Gooooooal

建议大家可以先去阅读两篇极品论文

1、IOI2004国家集训队论文——《后缀数组》（许智磊）

2、IOI2009 国家集训队论文——《后缀数组——处理字符串的有力工具》（罗穗骞）

一般理解这两篇论文之后并且能够实现倍增算法，那后缀数组也就应该可以算是打下基础了。我要说的只不过是自己的一些感悟和自己看得比较吃力的地方，希望对大家有所帮助。

关于一些定义以及性质（“//”注释符后面的为本人的笔记）：

后缀数组　后缀数组SA是一个一维数组，它保存1..n的某个排列SA[1],SA[2],...SA[n]，并且保证Suffix(SA[i])<Suffix(SA[i+1]),1≤i<n。也就是将S的n个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA中。（1）

//这里对后面的k-后缀数组的定义起了决定性的作用。

名次数组　名次数组Rank=SA^-1，也就是说若SA[i]=j，则Rank[j]=i，不难看出Rank[i]保存的是Suffix(i)在所有后缀中从小到大排列的“名次”。（2）

//名次数组也在一定程度上结识了后缀数组的“成分”。

k-后缀数组SA_k保存1..n的某个排列SA_k[1],SA_k[2],…SA_k[n]使得Suffix(SA_k[i]) ≤_kSuffix(SA_k[i+1]),1≤i<n。也就是说对所有的后缀在k-前缀比较关系下从小到大排序，并且把排序后的后缀的开头位置顺次放入数组SA_k中。

//也就是该后缀的长度为k。结合（1）

k-名次数组Rank_k，Rank_k[i]代表Suffix(i)在k-前缀关系下从小到大的“名次”，也就是1加上满足Suffix(j)<_kSuffix(i)的j的个数。通过SA_k很容易在O(n)的时间内求出Rank_k。

//同上。

倍增算法(Doubling Algorithm)，它正是充分利用了各个后缀之间的联系，将构造后缀数组的最坏时间复杂度成功降至O(nlogn)。

对一个字符串u，我们定义u的k-前缀

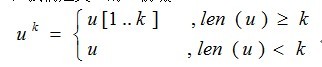
定义k-前缀比较关系<_k、=_k和≤_k：

设两个字符串u和v，

u<_kv　当且仅当　u^k<v^k

u=_kv　当且仅当　u^k=v^k

u≤_kv　当且仅当　u^k≤v^k

直观地看这些加了一个下标k的比较符号的意义就是对两个字符串的前k个字符进行字典序比较，特别的一点就是在作大于和小于的比较时如果某个字符串的长度不到k也没有关系，只要能够在k个字符比较结束之前得到第一个字符串大于或者小于第二个字符串就可以了。

根据前缀比较符的性质我们可以得到以下的非常重要的性质：

性质1.1　对k≥n，Suffix(i)<_kSuffix(j)　等价于　Suffix(i)<Suffix(j)。

性质1.2　Suffix(i)=_2kSuffix(j)等价于

Suffix(i)=_kSuffix(j) 且Suffix(i+k)=_kSuffix(j+k)。

//要使2k长的后缀相等，可以理解为分别从i、j开始的长度为k的后缀相等，且分别从i+k、j+k开始的长度为k的后缀相等。反之，依然。

性质1.3　Suffix(i)<_2kSuffix(j) 等价于

Suffix(i)<_kSuffix(j) 或 (Suffix(i)=_kSuffix(j) 且Suffix(i+k)<_kSuffix(j+k))。

//原理同上。

　　这里有一个问题，当i+k>n或者j+k>n的时候Suffix(i+k)或Suffix(j+k)是无明确定义的表达式，但实际上不需要考虑这个问题，因为此时Suffix(i)或者Suffix(j)的长度不超过k，也就是说它们的k-前缀以'$'结尾，于是k-前缀比较的结果不可能相等，也就是说前k个字符已经能够比出大小，后面的表达式自然可以忽略，这也就看出我们规定S以'$'结尾的特殊用处了。

//这一段可以说是倍增思想的源头，为什么可以用倍增思想？怎样将倍增思想用在后缀数组的构造上？

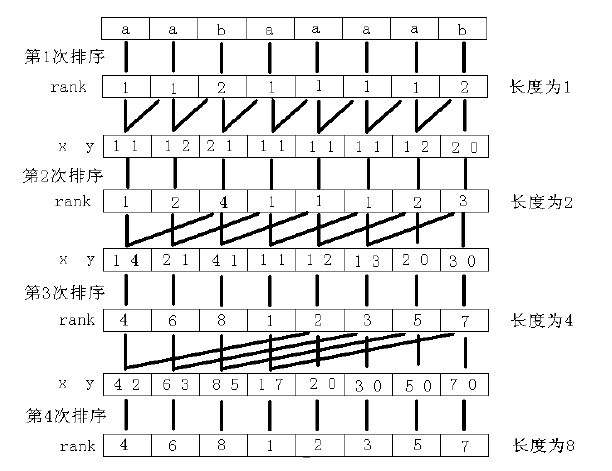
 ////看了罗同学的这张图，应该就可以理解倍增算法在构造后缀数组时起得作用了吧。

假设我们已经求出了SA_k和Rank_k，那么我们可以很方便地求出SA_2k和Rank_2k，因为根据性质1.2和1.3，2k-前缀比较关系可以由常数个k-前缀比较关系组合起来等价地表达，而Rank_k数组实际上给出了在常数时间内进行<_k和=_k比较的方法，即：

Suffix(i)<_kSuffix(j)　当且仅当　Rank_k[i]<Rank_k[j]

Suffix(i)=_kSuffix(j)　当且仅当　Rank_k[i]=Rank_k[j]

因此，比较Suffix(i)和Suffix(j)在k-前缀比较关系下的大小可以在常数时间内完成，于是对所有的后缀在≤_k关系下进行排序也就和一般的排序没有什么区别了，它实际上就相当于每个Suffix(i)有一个主关键字Rank_k[i]和一个次关键字Rank_k[i+k]。如果采用快速排序之类O(nlogn)的排序，那么从SA_k和Rank_k构造出SA_2k的复杂度就是O(nlogn)。更聪明的方法是采用基数排序，复杂度为O(n)。

求出SA_2k之后就可以在O(n)的时间内根据SA_2k构造出Rank_2k。因此，从SA_k和Rank_k推出SA_2k和Rank_2k可以在O(n)时间内完成。

下面只有一个问题需要解决：如何构造出SA₁和Rank₁。这个问题非常简单：因为<₁，=₁和≤₁这些运算符实际上就是对字符串的第一个字符进行比较，所以只要把每个后缀按照它的第一个字符进行排序就可以求出SA₁，不妨就采用快速排序，复杂度为O(nlogn)。

于是，可以在O(nlogn)的时间内求出SA₁和Rank₁。

//HDU 1403  Longest Common Substring中关于SA₁和Rank₁的构造

//花O(n)的时间对h=1进行基数排序
for(i=0;i<L;i++)
    B[szText[i]]++;
for(i=1;i<256;i++)
    B[i]+=B[i-1];
for(i=L-1;i>=0;i--)
    Suffix[--B[szText[i]]]=i;

//计算Rank(1),因为仅仅是1阶的Rank，所以有并列的
for(Rank[Suffix[0]]=0,i=1;i<L;i++)
{
    if(szText[Suffix[i]]==szText[Suffix[i-1]])
        Rank[Suffix[i]]=Rank[Suffix[i-1]];
    else
        Rank[Suffix[i]]=Rank[Suffix[i-1]]+1;
}


//Suffix数组即为SA1，Rank即为Rank1。

求出了SA₁和Rank₁，我们可以在O(n)的时间内求出SA₂和Rank₂，同样，我们可以再用O(n)的时间求出SA₄和Rank₄，这样，我们依次求出：

SA₂和Rank₂，SA₄和Rank₄，SA₈和Rank₈，……直到SA_m和Rank_m，其中m=2^k且m≥n。而根据性质1.1，SA_m和SA是等价的。这样一共需要进行logn次O(n)的过程，因此可以在O(nlogn)的时间内计算出后缀数组SA和名次数组Rank。